Vorlesung: Mi, 10-12; Raum 05-136 (3 LP)
Eine typische Fragestellung, die in dieser zweistündigen Vorlesung behandelt wird, ist wie folgt:
Gegeben eine holomorphe (d.h. komplex differenzierbare) Funktion f in der Einheitskreisscheibe; gesucht ist eine rationale Funktion r mit Polstellen außerhalb des Einheitskreises, die die gegebene Funktion auf dem Rand des Einheitskreises möglichst gut approximiert.
Solche Fragestellungen tauchen in den Ingenieurwissenschaften oft auf, etwa bei der Konstruktion stabiler dynamischer Systeme oder in der Signalanalyse.
Die bekanntesten Ansätze zur Konstruktion solcher rationaler Funktionen sind Padé-Approximationen, baryzentrische Interpolationsschemata sowie die Theorie von Adamjan, Arov und Krein. Die Vorlesung gibt einen Einblick in die Ideen sowie die zugrundeliegende Theorien hinter den entsprechenden Methoden und behandelt exemplarische Anwendungen.
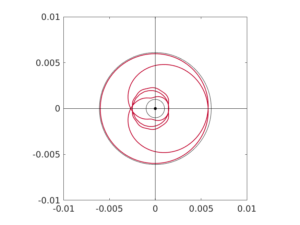
Als Appetitmacher zeigt die Abbildung in rot die Fehlerkurve (in der komplexen Ebene) einer konkreten Approximation durch eine rationale Funktion mit Zähler- und Nennergrad n=2. Diese Kurve ist das Bild der Einheitskreislinie unter der Funktion f-r. Man sieht, dass der Fehler durchweg betragsmäßig kleiner als 0.006 und größer als 0.001 ist (die Zahlen korrespondieren zu den Radien der beiden eigezeichneten Kreislinien), und die Windungszahl der Fehlerkurve um den Ursprung ist gleich 2n+1=5. Unter diesen Umständen kann man zeigen, dass der Fehler der bestmöglichen rationalen Approximation vom gleichen Grad n in der Supremumsnorm zwischen den genannten Schranken liegt.
Die Vorlesung richtet sich an Studierende aller mathematischen Studiengänge ab dem vierten Fachsemester. Grundkenntnisse in Funktionentheorie sind hilfreich.
Studienleistung
Für eine erfolgreiche Teilnahme an der Vorlesung gibt es zwei Optionen:
- regelmäßige Teilnahme (maximal ein unentschuldigtes Fernbleiben)
- 15-minütige mündliche Prüfung