| Type | Lecture Course |
| Lecturer | Prof. Dr. Martin Hanke-Bourgeois |
| Date |
Monday, 10 a.m.-12 p.m., Thursday, 2 p.m.- 4 p.m. |
| Room | 05-136 |
| Language | English |
| Credit Points | 6 cr |
Linear equations, for which the solution does not depend continuously on the data are called ill-posed according to Hadamard. Well-known examples include the Cauchy problem for elliptic partial differential equations and many notable auxiliary problems which arise in computerized tomography techniques.
In the language of functional analysis such problems arise, when the linear operator fails to have a bounded inverse in the appropriate Banach or Hilbert spaces - despite its injectivity. Or, to put it differently, that the range of this linear operator is not closed. It follows that this is an intrinsic infinite dimensional property which cannot be understood on the grounds of the basic linear algebra curriculum. Unfortunately, time does usually not permit to deepen the corresponding understanding in the basic functional analysis class, either. In particular, the implications for real-world problems are usually not discussed at all.
It is the purpose of this lecture course to step into the breach and to investigate possible pitfalls when dealing with ill-posed problems, ways to overcome these difficulties, and real-world examples for illustration, where these techniques are seen in action. The prerequisites are basic knowledge in functional analysis, i.e., Hilbert spaces, bounded linear operators, weak convergence, etc. The applications which occur as motivating examples include the aforementioned Cauchy problem, X-ray computerized tomography, impedance tomography, image deblurring, and inverse source problems for partial differential equations.
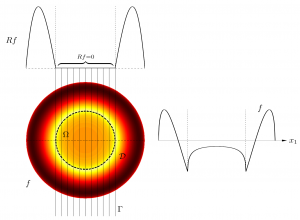
Radially symmetric “ghost” in computerized tomography
Textbooks:
A. Kirsch: An Introduction to the Mathematical Theory of Inverse Problems. Springer, New York, 2011.
A. Rieder: Keine Probleme mit Inversen Problemen. Vieweg, Wiesbaden, 2003.
M. Hanke: A Taste of Inverse Problems. Basic Theory and Examples. SIAM, Philadelphia, 2017.