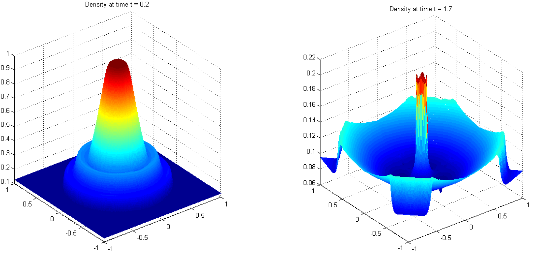
We deal with mathematical and numerical modelling of complex multi-dimensional systems of hyperbolic conservation laws. Models to be studied theoretically as well as experimentally include: nonlinear hyperbolic conservation laws, such as the Euler equations of fluid dynamics, the magnetohydrodynamic equations or the multi-phase flows. Some other models we shall like to consider are the system of conservation laws and balance equations governing the evolution of three dimensional nonlinear wave fronts and shock fronts respectively. Our aim is to use genuinely multi-dimensional schemes, such as the finite volume evolution Galerkin methods, upwind-based multi-dimensional Boltzmann methods as well as relaxation schemes.

The research is realized within the joint project with the group of Prof. Phoolan Prasad, Dr. S.V. Raghurama Rao and K.R. Arun from the Indian Institute of Science, Bangalore.
The project is supported by the German Academic Exchange Service (DAAD). For publications see [1],[2],[3],[4].

A circular expansion/ transonic flow computed by the FVEG scheme