Materials encountered in industry and medicine often fall outside the classical models of Newtonian viscous fluids. The class of non-Newtonian fluids is very broad. Examples of non-Newtonian fluids abound in every-day life. Multigrade oils, composite materials, polymers, liquid detergents, paints, printing inks and industrial suspensions all fall within this category as do biological fluids such as blood. The so-called multipolar fluids are characterized by dominant effects of nonlinear viscosity. In fact, their stress tensor depends not only on deformation tensor but also on higher order gradients of velocity.
Simple example of multipolar fluids is the so-called power-law fluid, for which the viscosity depends nonlinearly on the deformation tensor. This model can be used in order to describe shear-thickening as well as shear-thinning properties. The latter is a frequent property of many non-Newtonian fluids, for example blood, composite materials or polymers. It is well-known that for such fluids the local Reynolds number can increase dramatically which leads to difficulties in discretization as well as in solution of resulting algebraic systems.
The goal of this research project is to develop new, efficient and robust numerical schemes for engineering and biomechanical applications. As a basis for numerical experiments and further developments we have used programme packages FEATFLOW (University of Dortmund) as well as UG (University of Heidelberg). Analytical properties, such as existence, uniqueness and stability of weak solution, has been studied in cooperation with S. Necasova (Czech Academy of Sciences, Prague).
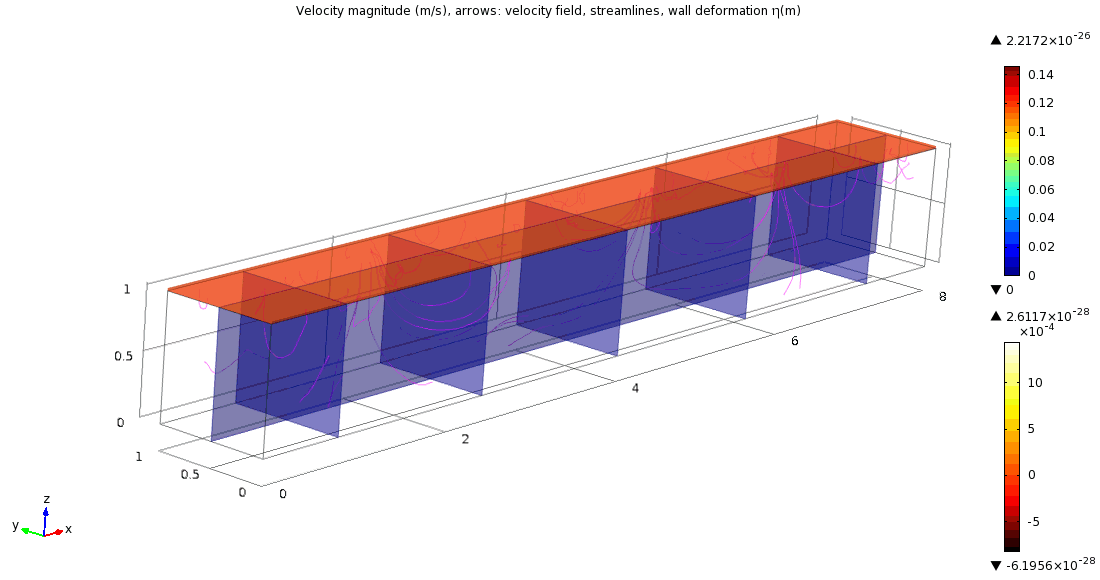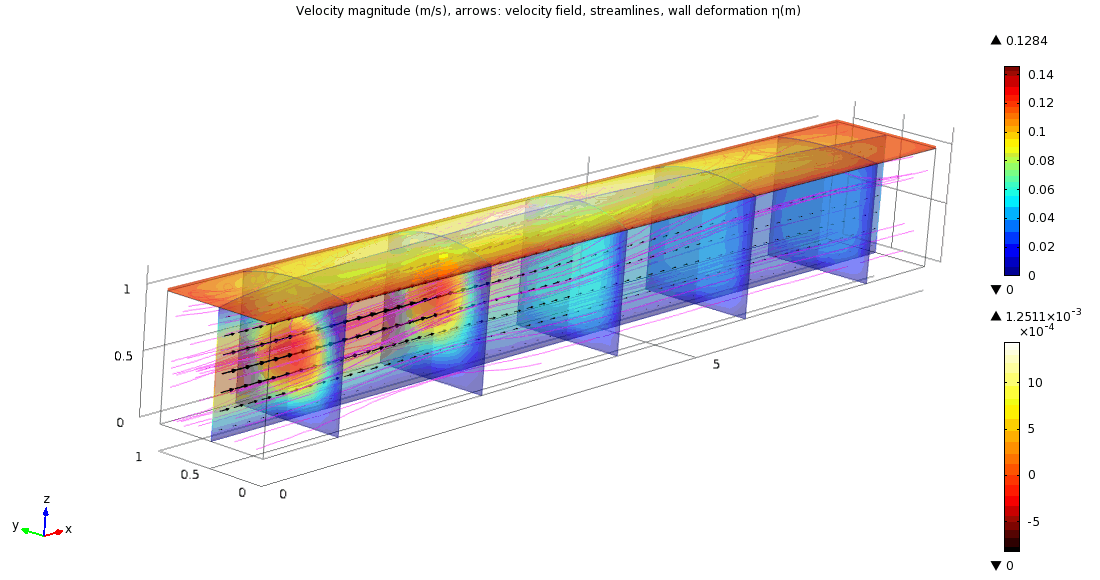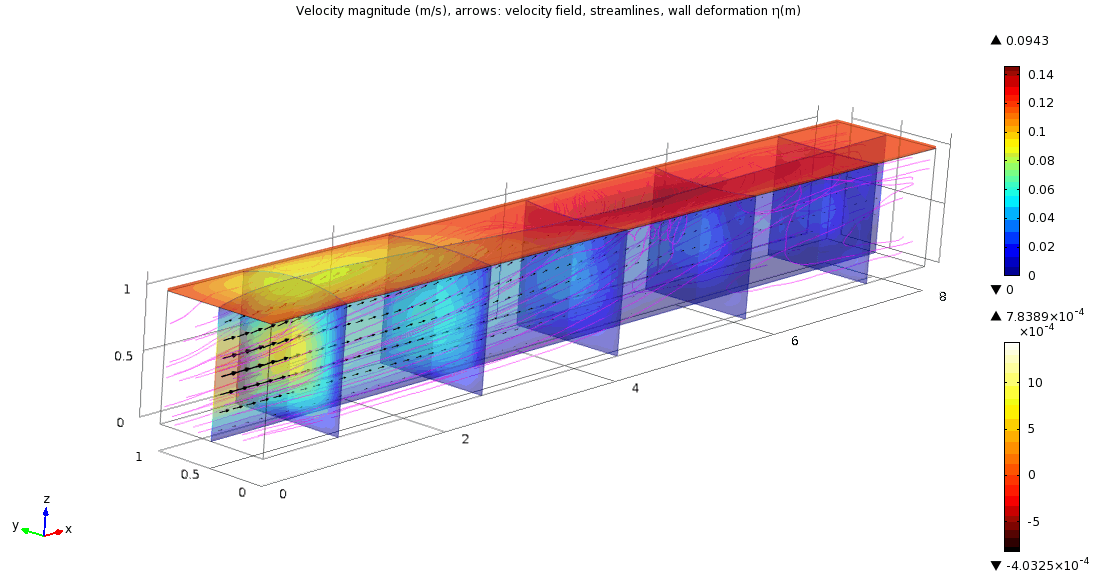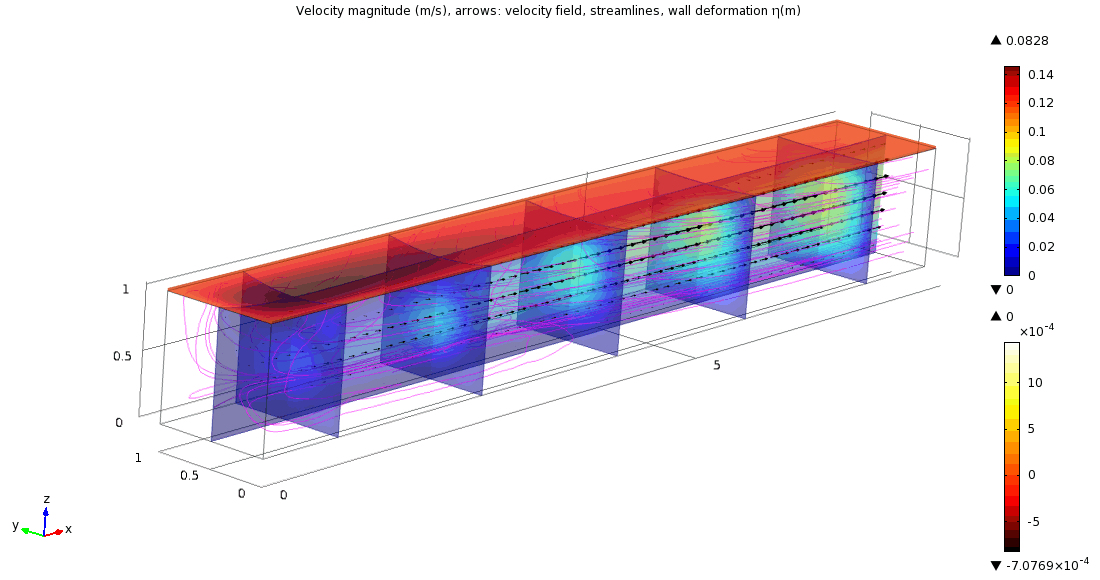
Our further aim within this research project is modelling of blood flow in elastic vessels that leads to fluid-structure interaction problems. This part of project is solved in cooperation with A. Hundertmark-Zauskova; supported by the EU-Project DEASE and by the German Science Foundation (DFG).
Numerical simulation of three-dimensional fluid flow and thin viscoelastic structure
(computed using the kinematic splitting algorithm by A. Hundertmark)